 本文採用線性代數的觀點分析, 指出: 今日許多大學所推動的 「教學品保」
其中的量化指標欠缺實質意義。 例如本系的 「教學品保量化指標」,
最多只有 0.3 位有效數字的意義。
略微改善之後也許可以提高到 0.7 位有效數字,
但受限於「許多數值是主觀判斷」的現實,
這也可能是多數現行 「教學品保量化指標」 的上限。
大學不應在沒有學理背景支持卻有許多爭議聲的情況下, 盲目推動教學品保,
還假裝這是很科學的管理方式。
不然我就想改行當一個巫醫或祈雨師算了。
本文採用線性代數的觀點分析, 指出: 今日許多大學所推動的 「教學品保」
其中的量化指標欠缺實質意義。 例如本系的 「教學品保量化指標」,
最多只有 0.3 位有效數字的意義。
略微改善之後也許可以提高到 0.7 位有效數字,
但受限於「許多數值是主觀判斷」的現實,
這也可能是多數現行 「教學品保量化指標」 的上限。
大學不應在沒有學理背景支持卻有許多爭議聲的情況下, 盲目推動教學品保,
還假裝這是很科學的管理方式。
不然我就想改行當一個巫醫或祈雨師算了。
一、 一組資料實例
一年半前我蒐集了一些 質疑教學品保的文章 並且自己也寫了一篇, 討論 教學品保與創意教學之間的矛盾。 這學期輪到我的課必須繳一份教學品保的報告。 與其把寶貴的生命浪費在一個具有爭議、 沒有學理基礎的盲目政策上面, 還不如認真地寫一篇揭發騙局的文章, 來當做我這學期的教學品保報告 :-) 也稟持著 (已經逐漸流失的) 學術精神, 提供所有相關的數據與檔案, 請大家指正本文的分析。
請下載我去年的科技英文課的教學品保量化指標 ods 檔 以及四個班的問卷結果統計檔: A、 B、 C、 N。 其實讀者可以從比較高的層次去理解它, 並不需要真的跟我一樣探究數學式的細節。 請看設計檔的 「授課大綱」 分頁就好。
首先, 每個系所都有一組自己設定的 「核心能力」。 例如本系的核心能力是:
- 管理知能於組織資源之運用能力
- 資訊技能於資訊系統之應用能力
- 專業倫理與團隊合作協調能力
- 資管相關時事議題認知與自主學習能力
再來, 每門課的授課教師必須設定幾個本課程的 「教學目標」。 例如我的科技英文的教學目標是:
- 英文閱讀能力
- 網路使用能力
- 閱讀習慣
- 中翻英能力
- 聽力
嗯, 讀者的笑聲我聽到。 這根本就是虛應敷衍下的產品。 後來新的規定是: 一位老師所寫的教學目標, 必須通過學群幾位老師的審核, 所以新版有改善; 而我也失去了更搞怪的機會。 (例如 「指出大學盲從微軟現象」 之類的教學目標) 不過, 我的教學目標寫得好不好並不是重點, 重點是: 它代表著異於 「系所核心能力」 的另一組指標。
最後, 請切換到 ods 檔的 「問卷」 分頁。 學生在學期末要填一份問卷。 如果老師沒有特別另外設計的話, 問卷題目就只是直接把教學目標抄過來小幅修改讓文句通順而已。
二、 向量空間模型
 假設每週上課的成果是一個向量 --
難以定義的無限多維向量空間當中的一個向量。
(嗯, 向量空間模型確實並不完全合理。 第五節 「本文分析方式的合理性?」
再回答這個問題。 提醒: 本文也算是
「行動歸謬證明法」。)
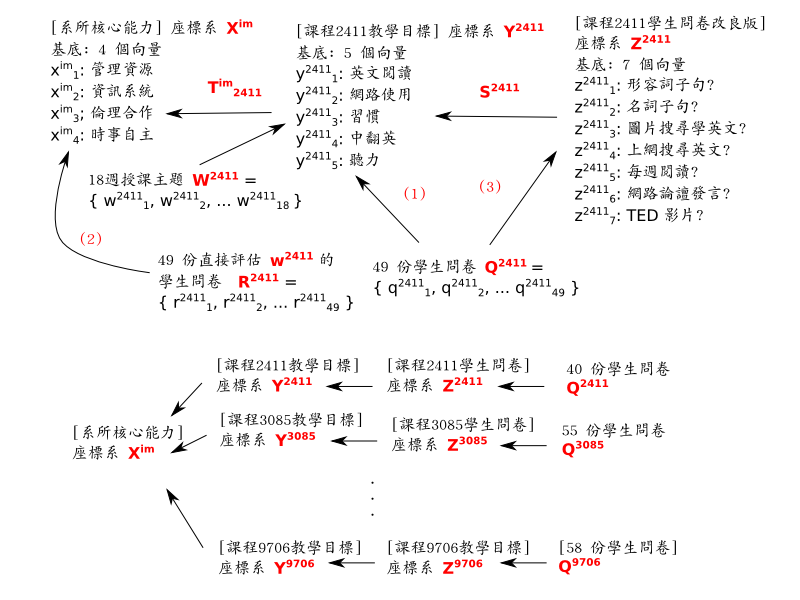
那麼在 ods 檔 「授課大綱」 分頁底下始於 A25 那格的對照表,
就是 18 個 「每週向量」 w24111,
w24112, ... w241118
分別在 「課程目標」 Y2411 這個五度子空間的投影 (的簡化版),
同時進行座標轉換 (改用 Y2411 的向量作為基底) 。
(所謂 "投影, 又進行座標轉換", 請想像
用 normal equation 求最小方差解; 以下類似)
另外, 在 「完全按照教學目標來設計問卷問題」 的簡單狀況下 --
也就是圖中紅字 (1) 的路線 -- 49 份學生問卷結果 q24111,
q24112, ... q241149
則是學生感受到的教學成果在 Y2411 子空間的投影/座標轉換 (的簡化版)。
假設每週上課的成果是一個向量 --
難以定義的無限多維向量空間當中的一個向量。
(嗯, 向量空間模型確實並不完全合理。 第五節 「本文分析方式的合理性?」
再回答這個問題。 提醒: 本文也算是
「行動歸謬證明法」。)
那麼在 ods 檔 「授課大綱」 分頁底下始於 A25 那格的對照表,
就是 18 個 「每週向量」 w24111,
w24112, ... w241118
分別在 「課程目標」 Y2411 這個五度子空間的投影 (的簡化版),
同時進行座標轉換 (改用 Y2411 的向量作為基底) 。
(所謂 "投影, 又進行座標轉換", 請想像
用 normal equation 求最小方差解; 以下類似)
另外, 在 「完全按照教學目標來設計問卷問題」 的簡單狀況下 --
也就是圖中紅字 (1) 的路線 -- 49 份學生問卷結果 q24111,
q24112, ... q241149
則是學生感受到的教學成果在 Y2411 子空間的投影/座標轉換 (的簡化版)。
至於 ods 檔同一分頁底下始於 A18 那格的對照表, 則是 「課程目標」 Y2411 五度子空間投影到系所 「核心能力」 Xim 四度子空間的投影矩陣 (的簡化版), 同時進行座標轉換 (改用 Xim 的向量作為基底)。 注意: 在這個 ods 檔的例子裡, 因為極度簡化, 矩陣 Tim2411只剩下一個 bit (0.3 位有效數字) 的資訊 ("有關聯" 或 "無關聯"),
同一分頁下, 始於 A12 那格的對照表, 其實就是十八週向量和 (或是平均值, 看你要不要把分母的常數考慮進去) 在 Xim 子空間的投影。 它是怎麼算出來的呢? 最複雜的 ods 檔 「相關聯結-關聯度」 分頁, 就是在把 w2411 = w24111 + ... w241118 投影到 Xim 並改用它的的基底來呈現。 首先, 始於 B15 的表格拿 w24111 ... w241118 來求和。 接著, 始於 J14 的表格拿 Tim2411 把 w2411 換成 Xim 的座標系。 再來, 始於 J4 的矩陣有正規化 (除以 18) 的效果。 最後, 始於 A2 的矩陣則只是把結果改用二維的表格來呈現 4 個 (1-5 共五種結果) 2.3 bit (0.7 位有效數字) 的座標值。 以上皆是指實際矩陣向量乘法的簡化版。 當然, 這些數字並不是 w2411 本身, 而是它在 Xim 的基底向量的投影的座標值。
顯然, 校方對於老師直覺估計所計算出來的 「以 Xim 的座標呈現 w2411 的投影」 不太有把握, 所以在四個班的問卷下方, 你可以看到學生們對同一向量的重新估計 -- 也就是圖中紅字 (2) 的部分 -- 被拿來跟老師的估計值做比較。
這些投影的目的, 是企圖要把一個系所開設的許多門課的大異其趣 w 向量, 通通投影到 Xim 同一個子空間當中, 採用一致的座標系, 然後才能做後續的量化處理。 如果可以拿到全系的資料、 拿到系報給學校的資料, 相信還是可以用線性空間的模型繼續進一步分析學校層級的 「教學品保量化指標」。
 以上複雜的分析是要給教學品保量化指標專家前來本文踢館用的,
裡面其實已經對支持者做了一些讓步。 (把 「十八週授課主題的加總或平均」
跟 「實際授課結果」 當成是不同的向量...諸如此類)
如果您本來就懷疑教學品保量化指標的客觀性與實質意義,
那麼請見
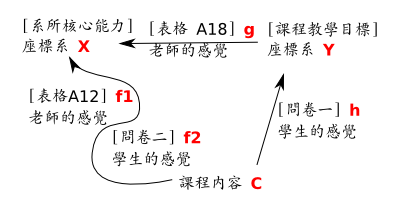
小格讀者 explorer 的精簡分析; 右圖是我依據他的分所所畫的。
以上複雜的分析是要給教學品保量化指標專家前來本文踢館用的,
裡面其實已經對支持者做了一些讓步。 (把 「十八週授課主題的加總或平均」
跟 「實際授課結果」 當成是不同的向量...諸如此類)
如果您本來就懷疑教學品保量化指標的客觀性與實質意義,
那麼請見
小格讀者 explorer 的精簡分析; 右圖是我依據他的分所所畫的。
三、 國王的新衣: 最多 0.3 位的有效數字
如果你還記得中學理化實驗裡的 「有效數字」 (易懂好文!) 概念, 「教學品保量化指標」 最令人難以下嚥的地方是: 以本系的例子來說, 最終數據的精確度, 不會超過一個 bit (0.3 位有效數字) -- 就算我們完全不質疑所有師生一切填寫數據的客觀性、 就算我們假設所有主觀填寫的數字都有無限多位有效數字, 單單是看 Tim2411 就知道: 任何通過它的結果 (每個 「科系」 層次的結果都必須通過它), 最多只能有一個 bit (0.3 位有效數字) 的精確度。
如果數學不是您的領域, 讓我做一個簡化版的比喻: 你要到克林貢星 (Klingon) 旅遊, 當地的導遊預估你需要準備 50000 克林貢幣左右。 但是在全宇宙之間, 克林貢星只跟瓦肯星 (Vulcan) 之間有貿易往來, 而克林貢幣與瓦肯幣之間的匯率, 大約在 30:1 到 60:1 之間。 (就像 Tim2411 一樣不夠精確) 瓦肯星幣跟美金之間的匯率, 有一個大致穩定的盤價。 請問你應該準備多少臺幣? 即使上文沒有詳細描述瓦肯星幣跟美金之間的匯率、 臺幣跟美金之間的匯率, 你也可以確定: 最終答案的不確定性至少將有上下高達兩倍的範圍。 也就是說, 任何有數學常識的人, 都不應該對最終算出來的那個數字存有太多不切實際的幻想。
這次, 國王就算真的有穿新衣, 那套新衣的大小, 恐怕要讓國王不露點都有困難。
四、 「教學品保量化指標」 更多無法回答問題
除了有效數字太少之外, 教學品保量化指標還有很多問題必須回答。 本文列出幾點, 如果有必要, 以後再另文詳細討論:
- [NC] 是不是應該要有負關聯性, 才能反應一些 「課程目標與系所核心能力背道而馳」 的事實? 例如某些課程 「Office 證照卓越」 的教學目標跟某些校系 「職業道德」 的核心能力, 兩者之間的夾角應該大於 90 度。 (彼此的投影量是負的。) 我知道大學不想承認; 但否認無法改變事實, 只會更加突顯量化指標沒有能力呈現這類大學不願面對的事實。
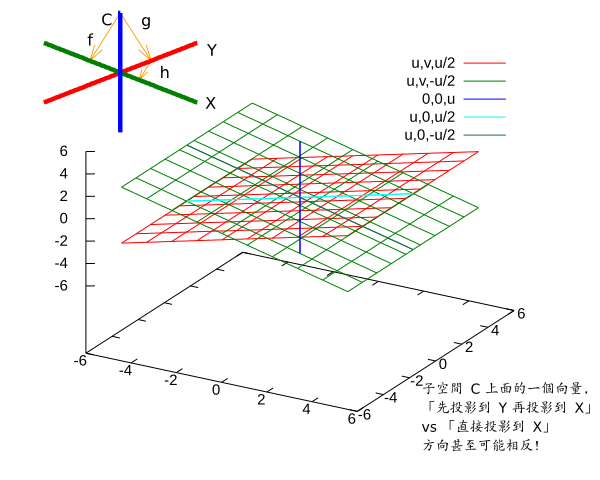 [MP] (請對照 explorer 簡化版的圖及右圖) 子空間 C 當中的一個向量,
「先投影到 Y 再投影到 X」 vs 「直接投影到 X」 這兩個結果可能大不相同,
甚至可能方向相反 -- 即使假設有效數字無限多位也一樣。
例如要把一張問卷結果 q241113
投影到 「系所核心能力」 子空間 Xim
再投影到院核心能力子空間, 如果分兩次算,
最終的結果甚至可能與原始向量夾角超過 90 度 (彼此的投影量是負的);
但如果直接投影, 那就保證不會超過 90 度。
[MP] (請對照 explorer 簡化版的圖及右圖) 子空間 C 當中的一個向量,
「先投影到 Y 再投影到 X」 vs 「直接投影到 X」 這兩個結果可能大不相同,
甚至可能方向相反 -- 即使假設有效數字無限多位也一樣。
例如要把一張問卷結果 q241113
投影到 「系所核心能力」 子空間 Xim
再投影到院核心能力子空間, 如果分兩次算,
最終的結果甚至可能與原始向量夾角超過 90 度 (彼此的投影量是負的);
但如果直接投影, 那就保證不會超過 90 度。
- [RR] 一門課的實際教學成果, 在 「系所核心能力」 子空間 Xim 的投影, 到底應該用紅字 (1) 再用 Tim2411 來求, 還是要直接套用紅字 (2)? 注意: 除了上述 [MP] 的考量之外, 在這裡, 兩者甚至是來自不同人的估計。 如前所述, 紅字 (2) 的路線可能比較有利漂亮的數據。 不僅如此, 因為它來自眾多學生的主觀判斷 (四個班問卷結果下方數據) (而不是單一老師的主觀判斷), 所以還有另外一個好處: 學生人數每擴增成四倍, 就可賺到一個 bit 的有效數字。 但是這樣一來, 老師們應該會抗議自己的專業判斷被學生蓋臺。 奇妙的是, 學校並沒有公佈這個問題的答案, 而老師們完全不知道學校的計算方式, 卻也沒有發出抗議的聲音。
- [IQ] 不過另一個考量, 會讓上一個問題得到完全相反的答案。 本系剛經過大學評鑑自評, 其中有委員希望我們改進問卷設計。 我不是很確定委員的意思; 不過如果委員的意思是 「問卷不要直接抄教學目標」, 那麼就需要多一層投影/座標轉換, 改走圖中紅字 (3) 的路線, 變成總共進行兩次投影/座標轉換, 前後參考了三個 (!) 不同的基底。 這也許會讓學生的直接回答更有意義, 但另一方面卻會讓投影結果偏離原始向量更遠, 也多增加一個降低有效數字的機會。 此外, 用來描述 「每個問題與每個教學目標之間關聯度高低」 的轉換矩陣 S2411, 當然也必須由每位授課老師自行設計, 沒有人可以代勞。 這應該也會引起老師的抗議。
- [XB] 如果一位授課老師 (透過填寫 W2411 間接) (謙虛地) 表示: 「我這門課對於系所核心能力 Xim3 『倫理合作』 沒有太大幫助啦」 但是學生問卷紅字 (2) 的結果, 卻是大有貢獻, 那麼這算是好事 ("意外的收穫") 還是壞事 ("偏離教學品保所設定的目標")? 兩者都不太合理; 但事關教師權益與對應策略設定, 校方應該明確回答這個問題。
- [IG] 教學品保量化指標完全無法呈現那些 「投影過程中, 被忽略掉的垂直分量」。 也就是說, 教學品保量化指標可能會鼓勵教師放棄那些 「與系所核心能力無關, 但很可能對於教育具有重大意義」 的教學面向。
我個人認為: 教學品保企圖以有限維度的量化指標搭配主觀的關聯性認定, 來描述複雜的人與人教學互動、 來描述主觀設定的各級 (校/院/系/學科) 目標, 這是完全不切實際的事、 這完全是在糟蹋數學, 藉數學之名舉辦的口號複誦大會。 (希望不是藉數學之名行控制教師巫毒術之實的邪惡技倆。) 這也是為什麼上面的問題令人難以回答, 左也不是, 右也不是。
五、 本文分析方式的合理性?
向量空間當然不是最完美的模型, 但它是所有可能模型當中, 一個夠通盤又夠簡單的折衷。
一方面, 它已經通用到足以將絕大多數的 「教學品保量化指標」 計算方式都視為是它的簡化版。 事實上, 我很有興趣蒐集更多各校系教學品保量化指標的計算公式與實例, 來證實以上這句話。 如果提供者同意具名或匿名讓我刊出分析結果, 我很樂意重複上一節的方式, 從向量空間投影/座標轉換的角度, 代為分析貴校貴系的量化指標, 並且指出你所能信賴的有效數字上限。
另一方面, 向量空間簡單到足以讓所有理、 工、 管理教師採用共同的語言 -- 線性代數 -- 來討論 「教學品保量化指標」 的困境。 任何教過線性代數、 微分方程、 工程數學、 管理數學、 多變量分析、 ... 的老師, 都可以用豐富精確的數學語言來討論 「教學品保量化指標」 的真實意義, 而不再需要像現在各校的教學品保一樣打迷糊仗、 「教學品保量化指標的意義, 長官說了算」。
如果堅持要採用最通用、 最完整、 涵蓋所有可能性的模型來分析, 也許就必須訴諸 metric tensor in curvilinear coordinates (曲線座標系的度規張量)。 我第一個承認這超出我的數學能力範圍。 但即使是用 metric tensor 來分析, 也一樣要面對投影流失資訊等等的問題, 上面所提的準確度問題恐怕只會更嚴重而不會更容易南忽略。 更重要的是: 「教學品保量化指標」 這整套系統當中含有這麼多主觀自由心證判斷所產生的 「相關程度」 數值, 本身已有太多的不確定性, 值得我們拿那麼複雜的數學工具來分析嗎?
有人會指出: 「0.3 位有效數字, 是你們系上的教學品保量化指標沒設計好; 如果設計得好, 可以有更多位的有效數字。」 這句話也許有一部分正確吧。 如果把 ods 檔 「授課大綱」 分頁的 A18 起的對照表改成 1 (低度相關) 到 5 (高度相關) 的 5 個等級, 再重新修改一些算式, 那麼精準度上限也許可以提高到 0.7 位有效數字。 (當然, 老師們也會抗議表格越改越囉嗦。) 至於那些 「比五個等級更細」 的區分法, 不僅不實際, 也很難有說服力好嗎? 再來, 姑且不論其他爭議, 單就提高有效數字的效果來看, 第四節的 [RR] 已指出: 採取紅字 (2) 路線, 有助於提升有效數字。 以64人的班來算, 大約可以得到 3 bits (0.9 位有效數字) 的準確度。 如果有哪一所校系不顧老師的抗議而這麼做, 或是有其他更好的解決方案, 那麼請仿本文, 完整分享你們的高精準度量化指標設計。 (但請不要採用 佈有專利地雷的 xlsx 格式。) 在那之前, 0.7 位有效數字的上限, 可能是所有現行教學品保校系所不得不面對的困窘現實。
但不論任何研究如何改良, 只要 「教學品保量化指標的敘述」 跟 「學生問卷的問題」 之間的轉換必須依靠 (學生/老師/校方) 主觀判斷給分, 有效數字就永遠不可能太高。 相對地, 未經投影與座標轉換、 一次到位的傳統 「學生對老師表現教學評量」 問卷 (或是只涉及長度/重量/貨幣/...等等明確單位轉換的後續處理) 就不會出現本文所指出來的這些問題。
六、 結論
別忘了, 最終, 「提出一個具有說服力數學模型」 的責任, 落在倡議教學品保的校方 (或是暗中操弄又推卸 accountability 的教育部) 肩上。 如果校方要以管理科學的偉大旗幟來推動教學品保, 那麼就應該先找到足夠的學理支持來背書, 或者最起碼提供一個範例, 說明如何設計一個精確度高於 0.7 位有效數字的量化指標, 並且以同儕評審的學術精神公開範例相關資料, 一方面讓大眾檢驗、 一方面將貴校系的優質設計分享給其他校系學習。 科學實驗與科學方法應該要可以讓讀者模仿重複; 不然就不叫科學了, 對吧?
如果大力推動教學品保的 逢甲大學、 元智大學、 銘傳大學、 長庚大學、 朝陽科大 等等大學, 對於 「教學品保量化指標 0.7 位有效數字上限」 無法提出一個有效的回應與駁斥, 甚至無法提供一個好的範例, 卻還是堅持繼續推動, 那麼我們大學學術界腐壞失聰失明的狀況, 恐怕遠比彭明輝教授所點出的 「全球大學排名 騙倒一堆校長」 要更可怕。 到時候, 我可能需要考慮改行當巫醫或是祈雨師之類的, 也許還比留在大學當教授更能夠維持理性思考的習慣和科學研究實事求是的精神。 至少這些行業不必透過糟蹋數學來假裝自己很科學。
* * * * *
(留言時, 請用 tex 語法表示上標下標, 例如 w241118 請寫成 「w^{2411}_{18}」。 集合、 矩陣/線性變換用大寫; 個別向量用小寫。)
(本文也刊載於 泛科學)
手邊沒電腦; 口頭推薦本文嗎? 可以請您的朋友搜尋 「教學品保量化指標」 或 「教學品保 騙局」。
![[rss feed 圖案]](/~ckhung/i/rss.png)