點與線的對偶關係
相對於單位圓的對偶關係
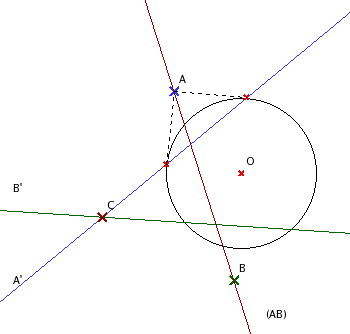 平面上有一個點 A = (xA, yA) (圖中藍色點),
我們定義它的 對偶 dual A' 為這條直線: xA x +
yA y= 1 (圖中藍色直線)。 反過來, 如果已知一直線 L
的方程式為 a x + b y = 1, 則定義它的對偶為 (a,b) 這個點。
平面上有一個點 A = (xA, yA) (圖中藍色點),
我們定義它的 對偶 dual A' 為這條直線: xA x +
yA y= 1 (圖中藍色直線)。 反過來, 如果已知一直線 L
的方程式為 a x + b y = 1, 則定義它的對偶為 (a,b) 這個點。
如果你的電腦裝有 drgeo, 則可以用 drgeo 打開 circ_dual.fgeo 這個檔, 逐一驗證下面所列的定理; 如果沒有, 就憑想像力與數學感來體會吧! 前幾個定理只談到一個點, 觀察時可以只拉動藍點, 並注意藍點與藍線的相對位置就好, 不要理會其他點/線。
- 圓內側一點 A, 其對偶直線 A' 完全落在圓外側。
- 圓上一點 A, 其對偶直線 A' 與圓相切, 且切點恰好就是 A。
- 圓外側一點 A, 其對偶直線 A' 通過圓內側。 由 A 向圓作切線, 兩切點連線恰為 A'。
- 離圓心越遠的點 A, 其對偶 A' 離圓心越近; 反之亦然。 當 A 趨近於圓心時, A' 趨近於無窮遠。
- 兩點 A 與 B 連線的對偶 C, 恰為其對偶 A' 與 B' 兩線的交點
相對於拋物線的對偶關係
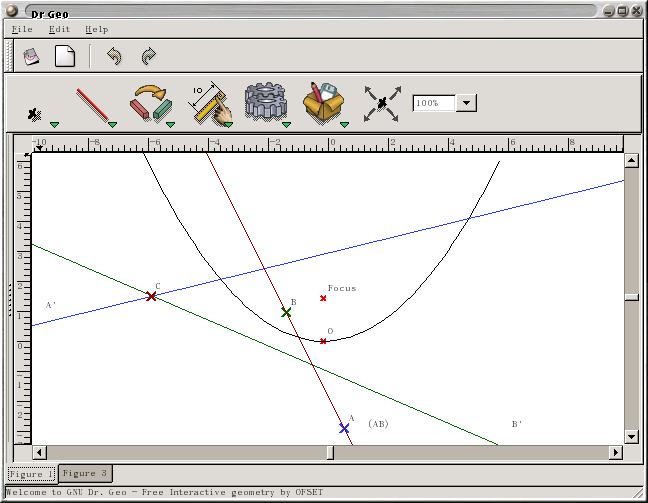 同樣的觀念, 現在改用拋物線來取代圓, 效果類似。 平面上有一個點 A =
(xA, yA) (圖中藍色點), 我們定義它的 對偶
dual A' 為這條直線: y = xA x - yA
(圖中藍色直線)。 反過來, 如果已知一直線 L 的方程式為 y = a x + b,
則定義它的對偶為 (a,-b) 這個點。
同樣的觀念, 現在改用拋物線來取代圓, 效果類似。 平面上有一個點 A =
(xA, yA) (圖中藍色點), 我們定義它的 對偶
dual A' 為這條直線: y = xA x - yA
(圖中藍色直線)。 反過來, 如果已知一直線 L 的方程式為 y = a x + b,
則定義它的對偶為 (a,-b) 這個點。
- 拋物線上側一點 A, 其對偶直線 A' 完全落在拋物線下側。
- 拋物線上一點 A, 其對偶直線 A' 與拋物線相切, 且切點恰好就是 A。
- 拋物線下側一點 A, 其對偶直線 A' 通過拋物線上側。 由 A 向拋物線作切線, 兩切點連線恰為 A'。
- 越低下的點 A, 其對偶 A' 越高; 反之亦然。 當 A 趨近於拋物線心時, A' 趨近於無窮遠。
- 兩點 A 與 B 連線的對偶 C, 恰為其對偶 A' 與 B' 兩線的交點
Convex Hull 與 Half-plane Intersection 問題互為對偶
![[Convex Hull 與 Half-plane Intersection 問題互為對偶] 圖案](ch_hpi.png) 這個圖由 ch_hpi 這個程式產生。
圖中灰色拋物線為 y = x^2/2, 灰點為原點; 其餘點 (稱它為 S 好了)
為我們計算 convex hull 的對象。 我們特地將有顏色的點放到 S
的上下左右四側。 令 S' 表示 S 裡面所有點的對偶線所成集合,
也就是說 S' 是圖中所有黑色直線加上四條彩色直線。 注意 S 的
upper hull 如何 (有順序地) 對應到 S' 的 lower envelope;
而 S 的 lower hull 如何對應到 S' 的 upper envelope。
這個圖由 ch_hpi 這個程式產生。
圖中灰色拋物線為 y = x^2/2, 灰點為原點; 其餘點 (稱它為 S 好了)
為我們計算 convex hull 的對象。 我們特地將有顏色的點放到 S
的上下左右四側。 令 S' 表示 S 裡面所有點的對偶線所成集合,
也就是說 S' 是圖中所有黑色直線加上四條彩色直線。 注意 S 的
upper hull 如何 (有順序地) 對應到 S' 的 lower envelope;
而 S 的 lower hull 如何對應到 S' 的 upper envelope。
- 本頁最新版網址: https://frdm.cyut.edu.tw/~ckhung/b/ma/duality.php; 您所看到的版本: February 14 2012 02:32:25.
- 作者: 朝陽科技大學 資訊管理系 洪朝貴
- 寶貝你我的地球, 請 減少列印, 多用背面, 丟棄時做垃圾分類。
- 本文件以 Creative Commons Attribution-ShareAlike License 或以 Free Document License 方式公開授權大眾自由複製/修改/散佈。
![[rss feed 圖案]](/~ckhung/i/rss.png)