從部分資訊求解
其實只需要很少的資訊, 就可以用普通的矩陣計算機 (例如 octave) 求出 optimal solution 及 shadow price。
Augmented Form
Augmented form (Slack form):
Maximize cT x
Subject to A x = b
Where x >= 0
如何將一般的問題轉換成 augmented form? 遇到小於等於的不等式, 就補上 slack variable; 遇到大於等於的不等式, 就補上 surplus variable。 例如 farmer.lp 一題, 補上三個 slack variables 之後, 變成:
max: 143 wheat + 60 barley;
capital: 120 wheat + 210 barley + s1 = 15000;
storage: 110 wheat + 30 barley + s2 = 4000;
land: wheat + barley + s3 = 75;
又如 tucker.lp 一題, 為前兩個條件補上 slack variables 並為第三個條件補上一個 surplus variable, 變成:
min: 15 f1 +10 f2 + 9 f3 + 7 f4;
labor: 2 f1 + 3 f2 + 4 f3 + 5 f4 + s1 = 3300;
material: 3 f1 + 4 f2 + 5 f3 + 6 f4 + s2 = 4000;
contract: f3 - s3 = 400;
delivery: f1 + f2 + f3 + f4 = 1000;
發生在頂點的事
 把一個線性規劃問題化為 augmented form 之後,
假設它有 m 條限制條件, n 個變數。 (當然 m < n) 例如 farmer.lp 的
m=3, n=5; tucker.lp 的 m=4 n=7。 在每個 corner point solution,
通常有 m 個變數的值不為 0, 這些變數叫做此處的 basic
variables; 另外 n-m 個變數的值為 0, 稱為此處的 non-basic
variables。 (在某些退化的情況下 (degenerate cases), 0
值的變數會超過 n-m 個, 不過遇到這種退化情況的機率接近 0,
而且本講義不談太多理論, 因此以下只討論一般狀況。) 反之亦然:
若已知某一組 feasible solution 其中的 m 個變數為 0, 則它必是一個
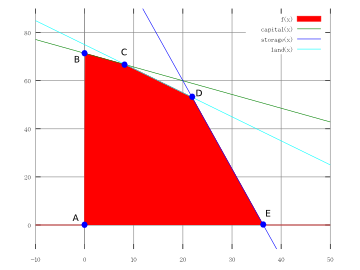
corner point solution。 例如在 farmer.lp 一題的圖中, A 對應到的
basic variables 是 s1,s2,s3; C 對應到的 basic variables 是
wheat,barley,s2; 而最佳解 D 對應到的則是 wheat,barley,s1。 Q:
那請問 B 與 E 分別對應到那兩組 basic variables?
把一個線性規劃問題化為 augmented form 之後,
假設它有 m 條限制條件, n 個變數。 (當然 m < n) 例如 farmer.lp 的
m=3, n=5; tucker.lp 的 m=4 n=7。 在每個 corner point solution,
通常有 m 個變數的值不為 0, 這些變數叫做此處的 basic
variables; 另外 n-m 個變數的值為 0, 稱為此處的 non-basic
variables。 (在某些退化的情況下 (degenerate cases), 0
值的變數會超過 n-m 個, 不過遇到這種退化情況的機率接近 0,
而且本講義不談太多理論, 因此以下只討論一般狀況。) 反之亦然:
若已知某一組 feasible solution 其中的 m 個變數為 0, 則它必是一個
corner point solution。 例如在 farmer.lp 一題的圖中, A 對應到的
basic variables 是 s1,s2,s3; C 對應到的 basic variables 是
wheat,barley,s2; 而最佳解 D 對應到的則是 wheat,barley,s1。 Q:
那請問 B 與 E 分別對應到那兩組 basic variables?
在頂點處, 因為 non-basic variables 的值為 0, 方程組可以簡化: 把所有對應到 non-basic variables 的那些行 (「直行橫列」) 全部刪除, 剩下一個 m 元線性聯立方程組, 用線性代數的方法 (例如 高斯消去法), 就可解出此處所有 basic variables 的值。 例如 farmer.lp 的 C 點座標可以這樣算:
A = [120,210; 110,30; 1,1]
b = [15000; 4000; 75]
c = [143; 60]
# 以上是原始題目
K = [A,[0;1;0]]
inv(K)*b
算出來的 8.33, 66.67, 1083.33 分別就是 C 點的 wheat,barley,s2 的值。
計算 shadow prices
最佳解一定是一個 corner point solution, 所以上述計算方式當然也適用於最佳解。 更方便的是, shadow prices 其實可由這個簡單的公式: y = B-T c 算出, 其中方陣 K 是由 「對應到 basic variables 的那些行」 所構成的。 例如 farmer.lp 的最佳解所對應到的 basic variables 是 wheat, barley, s1, 所以它的 shadow prices 可以這樣算:
K = [A,[1;0;0]]
cb = [c; 0]
inv(K)'*cb
又如 tucker.lp 的最佳解所對應到的 basic variables 是 f1, f2, f3, s1, 所以它的 shadow prices 可以這樣算:
A = [3,6,5,4; 2,5,4,3; 0,0,1,0; 1,1,1,1]
b = [4000; 3300; 400; 1000]
c = [15; 7; 9; 10]
# 以上是原始題目
K = [A(:,[1,3,4]),[0;1;0;0]]
cb = [c([1,3,4]);0]
inv(K)'*cb
作業: 請用 lp_solve 解 ex1.lp 及 ex2.lp 並記下那些變數是 basic variables。 再用 octave 求出最佳解的值及 shadow prices, 並和 lp_solve 所解出來的答案對照一下。
- 本頁最新版網址: https://frdm.cyut.edu.tw/~ckhung/b/lp/partial.php; 您所看到的版本: February 14 2012 02:32:25.
- 作者: 朝陽科技大學 資訊管理系 洪朝貴
- 寶貝你我的地球, 請 減少列印, 多用背面, 丟棄時做垃圾分類。
- 本文件以 Creative Commons Attribution-ShareAlike License 或以 Free Document License 方式公開授權大眾自由複製/修改/散佈。
![[rss feed 圖案]](/~ckhung/i/rss.png)