簡介
例題一: 種什麼才好?
請見 lpsolve 手冊 的這一篇: "Formulation of an lp model in lpsolve"。 摘要: 農夫有 75 畝地, 可種 wheat 或 b。 wheat 的成本每畝 $120, barley 的成本每畝 $210。 農夫資本額 $15000。 wheat 產量每畝 110 桶, barley 產量每畝 30 桶, 農夫的倉庫共可儲存 4000 桶。 wheat 的淨利是每桶 $1.3 而 b 的淨利是每桶 $2.0。 請問這 75 畝應該如何分配給這兩種作物以獲得最高利潤?
暫停往下看, 請先思考並寫出數學模型。 我們可以改變兩個變數, 來達成最高利潤; 但不能違背三個限制條件。 數學模型在 farmer.lp 檔案裡 (別急著點進去!)
用 lpsolve 解題
請安裝 lpsolve
(ubuntu 底下: sudo apt-get install lp-solve) 並執行 lp_solve
farmer.lp 印出以下結果:
Value of objective function: 6315.62
Actual values of the variables:
wheat 21.875
barley 53.125
用 octave 驗證
先複習一下 矩陣定義及矩陣乘法。 進入 octave, 逐列剪貼以下指令, 觀察列印結果並思考其輸出的意義:
A = [120,210; 110,30; 1,1]
b = [15000; 4000; 75]
c = [143; 60]
x = [21.875; 53.125]
c'*x
A*x
b-A*x
上面的 A,b,c 都是題目抄來的參數。 x 是從 lp_solve 解出的最佳解 (兩種作物各種多少) 抄來的。 c'*x 得到最佳利潤, 當然與 lp_solve 的答案要一樣。 A*x 是實際使用的資金, 倉儲, 與耕地。 b-A*x 則是未用完的資金, 倉儲, 與耕地。 從 b-A*x 的零值可看出: 在 optimal solution 處, binding constraints 為 storage (倉儲) 與 land (耕地)。
用 oocalc 或 gnumeric 解題
 安裝 OpenOffice.org,
並用其中的 oocalc 試算表工具開啟 intro.ods。 [或者安裝 gnumeric, 並開啟 intro.gnumeric。] 這個檔案裡面有兩個範例,
分別放在不同的分頁裡面。 請用底下的分頁標籤切換到 farmer 分頁。
安裝 OpenOffice.org,
並用其中的 oocalc 試算表工具開啟 intro.ods。 [或者安裝 gnumeric, 並開啟 intro.gnumeric。] 這個檔案裡面有兩個範例,
分別放在不同的分頁裡面。 請用底下的分頁標籤切換到 farmer 分頁。
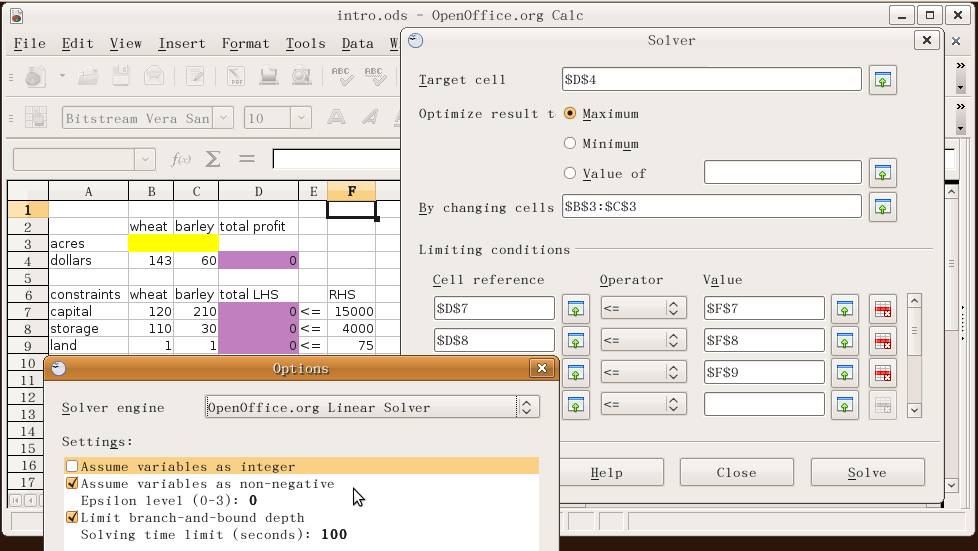
先看那兩個黃底的空白格 -- 等一下 oocalc [或 gnumeric] 的解題工具 solver 會在裡面試著填各種不同的數字。 假設 B3 裡面的數字代表 "要種幾畝 wheat", C3 裡面的數字代表 "要種幾畝 barley"。 其次看四個紫底格子 D4, D7, D8, D9 -- 等一下 B3 與 C3 在變動時, solver 會根據這四格的運算式, 自動更新這四格的數值。 點一下 D4, 請解釋為什麼這一格的運算式算出來的是總利潤? D7 是 「成本共多少元」; D8 是 「總共用掉多少桶的儲存空間」; D9 是 「總共用掉幾畝地」。 為什麼運算式裡有些地方有錢號, 有些沒有?
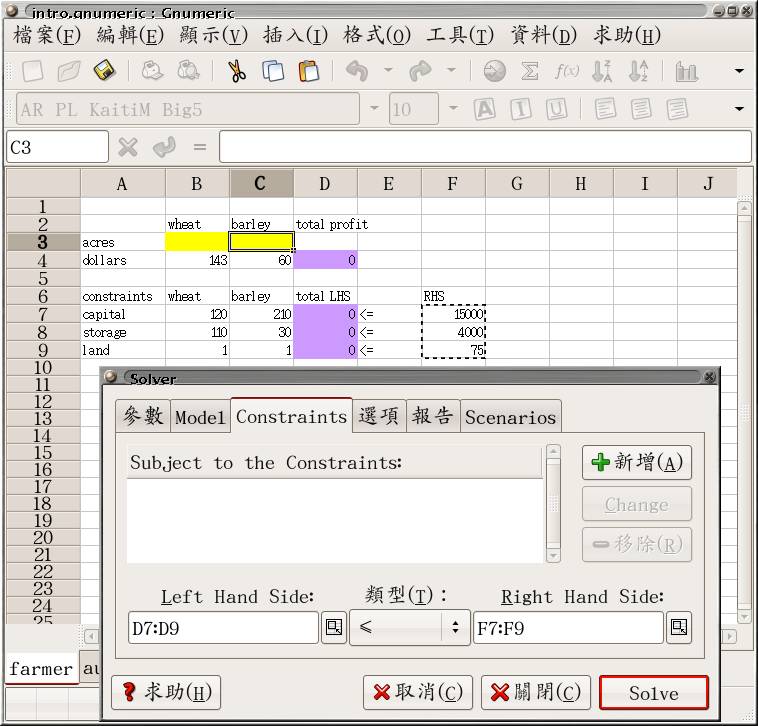 接下來從 tools 選單打開 solver 對話框, 叫出 oocalc [或 gnumeric]
的解題工具。 [若是 gnumeric, 要切換到 parameters 分頁]
把題目中的三個關鍵描述給 solver:
接下來從 tools 選單打開 solver 對話框, 叫出 oocalc [或 gnumeric]
的解題工具。 [若是 gnumeric, 要切換到 parameters 分頁]
把題目中的三個關鍵描述給 solver:
- variable (決策變數): 那幾格的數字是可以任意調整的? 點一下 By changing cells, 再到試算表選取 B3:C3 那兩個黃底的空白格。
- objective function (目標函數): 決策變數的目的, 是為了衝高 (或壓低) 那一個數字? 點一下 Target cell, 再到試算表點選 D4 那一格。
- constraints(限制條件): 改變決策變數時, 不可違背那些條件? 這一題有三個條件, 分別是 "D7 <= F7"﹑ "D8 <= F8"﹑ "D9 <= F9"。 把它們填到 oocalc 的 limiting conditions 底下, 或 gnumeric 的 Constraint 分頁裡面。 注意: 填左邊時, 可以一次選取 D7 到 D9 三格; 同樣地, 填右邊時, 可以一次選取 F7 到 F9 三格。 [gnumeric: 填完後, 記得要點選 Add (新增), 才會真的加入這一組 (共三個) 限制條件。]
自動解題之前, 還需要確認一下題目的類型。 目前我們只處理線性﹑ 且所有變數均大於等於零的狀況。 在 oocalc 裡面, 請點選 options, 勾選 "Assume variables as non-negative"; 在gnumeric 裡面, 請點選 Model 分頁, 勾選 Assume Non-Negative。
最後, 按下 solve, 注意 B3 與 C3 出現最佳耕地分配; D4 出現預期獲利; D7:D9 出現各種資源的實際使用情形。
例題二: 汽車子廠分工
改編自 Michael Trick 教授的講義。 摘要: Tucker 汽車公司將生產 1000 輛汽車。 Tucker 汽車公司有四個子廠, 每個廠生產一部汽車的成本不同; 所需使用的人時及原物料也各不相同, 如附表:
| 子廠 | 成本 | 原物料 | 工時 |
| A | 15 | 3 | 2 |
| B | 7 | 6 | 5 |
| C | 9 | 5 | 4 |
| D | 10 | 4 | 3 |
又因為契約因素, 這 1000 輛汽車當中, 至少有 400 輛必須交由 3 廠生產。 今共有 4000 原物料及 3300 人時可供支配, 請問應如何分配方能使成本降至最低? 模型請見 tucker.lp。
oocalc/gnumeric 試作: 一樣請打開先前的範例檔, 並切換到 auto-company 分頁。 試著完成此表格。 可從 farmer 分頁把數學式剪貼過來。 [gnumeric: 「滑鼠右鍵-copy」 之後, 一定要先按 ENTER 或 Escape, 以免 gnumeric 以為你要替此格選新的範圍。] 設定 solver 時, 除了敲入 constraint 之外, 還要記得此題與上題的目標相反...。
問題與討論: 「成本」 是否包含薪資及原物料? 「降低成本」 是否為最重要的目標? 算出數字很重要; 但檢討數學式是否精確反應現實, 更重要。
名詞 & 圖解
- objective function (目標函數): 例如
「種什麼才好?」 當中的利潤函數; 又如 「汽車公司的子廠分工」
當中的成本函數。
- variable (決策變數): 例如 「種什麼才好?」 當中的 wheat (要拿多大的面積種 w?) 與 barley (要拿多大的面積種 b?) 兩個變數; 又如 「汽車公司的子廠分工」 當中的 f1, f2, f3, f4 (每個子廠各要生產幾部汽車?)。 這些變數到底要調整/設定到什麼值, 才會得到最佳利潤或最低成本? 這就是線性規畫要討論的問題。
- constraint (限制條件): 就是依據題目所列出來的等式與不等式。 這些等式與不等式限制了決策變數能夠調整/設定的範圍。
- variable bound
- feasible solution (可行解): (決策變數的) 一組滿足所有限制的設定值。 例如 (wheat, barley) = (10, 30)
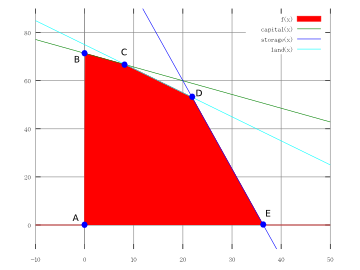
- feasible region (可行區域): 所有 feasible solutions 所成的集合, 例如右圖紅色部分。
- corner point solution: 座落於 feasible region 頂點的解。 例如右圖的 A,B,C,D,E 五個解都是。
- optimal solution: 例如右圖的 D。
- active constraints (binding constraints) (tight constraints): (在某一解處的) 等號成立的那些限制條件。 例如在 B 點的 binding constraint 只有一個: capital (資金); 而在 C 點的 binding constraints 則有 capital (資金) 與 land (耕地) 兩項。
作業
- 請用 lp_solve 解這題: steel.lp, 並分別用計算機與 octave 驗證 lp_solve 算出來的 optimal solution 確實是一個 feasible solution。 在此處, 那些限制條件是 binding constraints? 參考解答在本頁原始碼某處。
附錄: 筆記
(此節可忽略)
轉檔
- 取得 netlib 的測試資料集, 並先備份! (因為等一下要原地轉檔, 萬一失敗...)
- 編譯第一支轉檔程式 emps:
gcc -o emps data/emps.c(ubuntu: 要先安裝 build-essential 套件才能編譯) - 安裝 lp-solve 套件並閱讀 README.txt.gz, 搜尋 mps2lp, 瞭解如何使用第二支轉檔程式
- 列出所有資料檔名於 ~/listing 當中:
perl -000 -ne 'print if /MPS/' index | perl -ne 'print "$1\n" if m#file\s+lp/data/(.*)#' > ~/listing - 還有 kennington/ 子目錄底下的資料檔, 也解壓縮, 並且列出檔名:
gunzip kennington/*.gz ; find kennington/ -name '*-*' >> ~/listing - 批次轉檔:
for f in $(cat ~/listing ) ; do ~/emps < $f > ~/tmp.txt ; lp_solve -parse_only -mps ~/tmp.txt -wlp $f ; done
製圖
更多參考資料
- John W. Chinneck Introduction to Linear Programming 口語化, 平易近人的簡介
- Spyros Reveliotis. An Introduction to Linear Programming and the Simplex Algorithm
- 用試算表軟體 gnumeric 解線性規劃題目
- 本頁最新版網址: https://frdm.cyut.edu.tw/~ckhung/b/lp/intro.php; 您所看到的版本: February 14 2012 02:32:25.
- 作者: 朝陽科技大學 資訊管理系 洪朝貴
- 寶貝你我的地球, 請 減少列印, 多用背面, 丟棄時做垃圾分類。
- 本文件以 Creative Commons Attribution-ShareAlike License 或以 Free Document License 方式公開授權大眾自由複製/修改/散佈。
![[rss feed 圖案]](/~ckhung/i/rss.png)