應用實例: 重力加速度下的物體運動軌跡

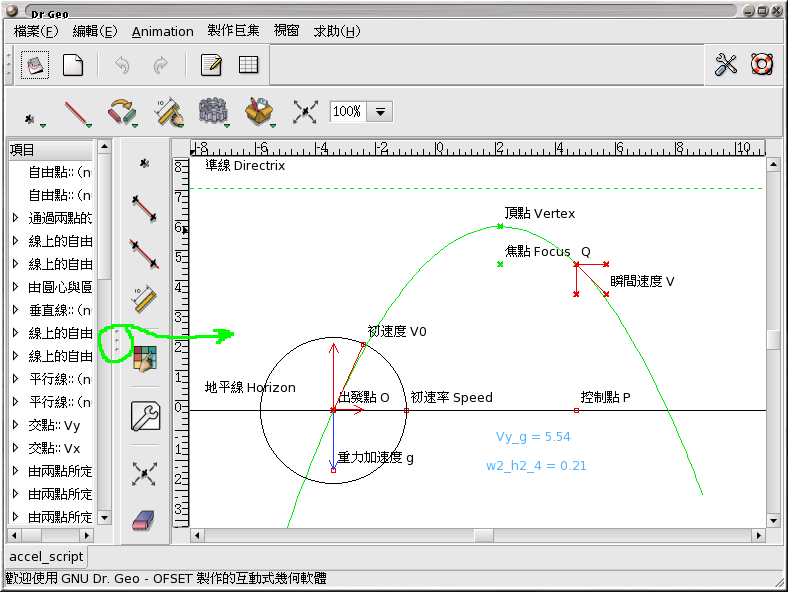
重力加速度下的物體運動軌跡

這一單元我們做一個較複雜的實用例子 -- 重力加速度下的物體運動軌跡, 如上圖。 也請用 Dr. Geo 把 fgeo 檔 打開, 並把視窗左緣向右拉, 在視窗左半部出現一片用文字表示的製圖過程。 也請用 「其他」 工具底下的 「外觀」, 把所有隱藏起來的製圖過程都打開來, 方便與以下步驟對照。

製圖步驟

  1. 畫一條水平線, 叫做 「地平線 Horizon」, 並把定義直線的兩個自由點隱藏起來, 以免等一下不小心把水平線拉歪了。
  2. 線上取兩個自由點, 一個叫做 「出發點 O」, 當做圓心; 另一個叫做 「初速率 Speed」。
  3. 以上述兩點畫圓, 並在圓上取一個自由點, 叫做 「初速度 V0」
  4. 過 O 做 Horizon 的垂直線叫做 L, 並在 L 上, Horizon 的下方取一自由點叫做 「重力加速度 g」。
  5. 畫出 V0 在 Horizon 的投影 Vx, 及 V0 在 L 的投影 Vy。 建立向量 O-Vx 與 O-Vy, 它們分別是 V0 的水平分量與垂直分量。
  6. 建立一個 scheme script 叫做 「頂點時刻 Top Time」, 它以 O-Vy 及 「重力加速度」 兩個向量為參數 (注意: 一定要向量; 不可以是線段) 並計算兩者的比值如下: 
            (define vy (cadr (getCoordinates a1)))
        (define g (cadr (getCoordinates a2)))
        (/ vy (/ g -5))
    這裡的 -5 倍, 主要在調整方向, 及縮小 g 的效果, 以方便拉取; 要改成 -3 或 -8 等等也可以。
  7. 以 O 為原點, 對 「速度的水平分量的端點」 進行縮放, 倍數為 「頂點時刻 Top Time」, 得到點 A。
  8. 過 A 做 Horizon 的垂直線, 這將是拋物線的對稱軸。
  9. 過 V0 做 Horizon 的平行線, 交對稱軸於點 B。 AB 也是 V0 的垂直分量。
  10. 再以 A 為原點, 對 B 進行縮放, 倍數一樣是 「頂點時刻 Top Time」, 得到點 C。 AC 的中點即是拋物線的頂點 Vertex。
  11. 定義線段 O-A 與線段 A-Vertex, 以此二者作為另一個 scheme script 「(w/h/2)^2」 的參數。 顧名思義, 就是要計算 "O-A 長度與 2 倍 A-Vertex 長度比值" 的平方: 
            (define w (getLength a1))
        (define h (getLength a2))
        (/ (* w w) (* h h 4))
  12. 以 Vertex 為原點, 對 A 進行縮放, 倍數為 「(w/h/2)^2」, 得到拋物線的焦點 Focus。
  13. 以 Vertex 為中心, 取 Focus 的點對稱, 得到點 D。 過 D 做 Horizon 的平行線, 即得到拋物線的準線 Directrix。
  14. 在 Horizon 上面取一個自由點, 叫做 「控制點 P」。 以 P 為自變量, 求出拋物線上一點 Q 作為應變點, 進而畫出拋物線。 (詳見 軌跡 一篇)
  15. 對 Q 施以平移, 以 V0 的水平分量為平移向量, 得到瞬間速度的水平分量。
  16. 畫出直線 Vy-A, 與直線 P-Q 交於點 R。 拿向量 P-R 來當做平移向量, 對 Q 施以平移, 即得到瞬間速度的垂直分量。

數學說明

為了畫出拋物線, 首先要找出拋物線頂點的位置。 假設出發時刻為 t=0, 到達頂點時刻為 t=tV, 則從初速度的垂直分量 Vy 可以求出 tV, 因為 Vy - g tV = 0。 所以在 tV 時刻, 物體已右移 Vx tV, 上移 Vy tV / 2。

眾所周知, 拋物線 y=k x^2 的焦點, 在 (0,k/4); 它的準線, 在 y=-k/4。 現在改以拋物線的頂點 Top 為原點, 用出發點 O 的 x,y 座標 (-w,-h) 來求得 k, 進而求得焦點距頂點 w^2/h/4。 我們用 script 計算 w^2/h^2/4, 所得的結果再拿來縮放 h。 (理由稍後解釋) 至此, 準線與焦點都很容易畫出, 也就可以畫出拋物線。

線上任意一點的瞬間速度呢? 水平分量保持不變, 很簡單; 垂直分量隨時間線性遞減, 怎麼算? 因為水平方向是等速度運動, 所以水平位置恰好可以拿來度量時間。 特別注意通過頂點的時刻, 垂直分量為 0, 所以直線 Vy-A 上面每一點距離地平線的高度, 恰好就是瞬間速度的垂直分量。

避免使用 「長度」 功能

一般說來, 建議盡量避免使用 「取線段長度」 的功能, 例如 「數值」 選單中的 「距離及長度」, 或是 script 中的 getLength 函數。 如果用了, 圖案就有可能只在某半部或某象限正確; 自由點一旦移出某個範圍, 圖案就會亂掉。 這很難描述, 不過你可以試試看不要按照這裡的步驟, 自己重畫這個圖, 並故意用到一兩次這類功能, 就會理解。 我重畫了很多遍, 經常沒有畫好, 只要初速度離開第一象限, 或重力加速度改變方向, 圖就亂掉。 拉動這些自變量, 直到圖案接近變亂界線時, 觀察那一條線段的長度接近 0, 可能就是那條線段的衍生物件或數字需要換一個方法做。 以本例當中的 「(w/h/2)^2」 script 為例, 如果改成計算 w/h/4, 再拿這個數字來縮放 w, 那麼當初速度進入第二, 四象限時, 拋物線就會畫錯 (猜的; 如果驗證出來請告訴我)。

怎麼樣才是正確的作法呢? 如果有三條線段 OA, OB, OC, 它們的長度分別為 a,b,c, 現在想找點 D, 使得 OD 的長度為 ab/c, 建議使用以下兩種方法之一:

  1. 像本例的第一個 script, 用 (cadr (getCoordinates ...)) 分別取得 向量 (不是線段) OA 與 向量 OC 的 y 座標, 求得比值, 再對向量或線段 OC 進行縮放。 這個方法有個小缺點: 當你的向量變成水平時, 可能會有一瞬間的閃失。 當然改 x 座標也可以, 意思一樣, 但閃失會出現在向量變成垂直時。
  2. 運用 「平行線截出等比例線段」 的特性, 求出 D。 請自行練習。

這是因為 「長度」 函數, 牽涉到絕對值, 而絕對值函數是有稜角的。 本例的第二個 script 雖然用到長度函數, 但是改成計算 (w/h/2)^2, 等同於沒有用到絕對值的算式, 所以可以畫出正確的圖形。

當初筆者繪製 最早版本 的 「重力加速度」 圖時, 還不會使用 scheme script, 一切都是用 「平行線截出等比例線段」 的方式, 計算出所有長度, 算是相當浩大的工程。