圖 (Graph) 的演算法

請複習 表達人事物之間的關係 與 Graph。 另外, 請用力玩 algotutor。

用 Queue 與 Stack 進行 Graph Traversal

問題: 如何將一個 graph 裡面的所有 vertices 都點名一遍? 這個動作叫做 graph traversal, 在更複雜進階的演算法裡面, 是一個常做的基本動作。

為避免重複點名浪費時間, 一路上必須記得那些 vertices 已經看過, 姑且稱這些已看過的 vertices 為 VISITED。 又, 每點到一個新的 vertex, 何妨順便將它的所有鄰居記錄下來。 這些 vertices 可能是我們未來點名的對象, 是搜尋過程當中, 開疆拓土的新邊境, 姑且稱之為 FRONTIER 或 FRINGE。 至於那些更遠的 vertices 呢? 當然叫做 "從來沒見過" UNSEEN 嘍。

這個演算法很簡單, 用一個資料結構 P 收納目前所有的 FRINGE vertices, 每次從裡面挑一個出來將它變成 VISITED, 同時介紹它所有的鄰居進入 FRINGE vertices。 當然, 一個鄰居如果本來就已經 VISITED 或 FRINGE, 就不必感化它了。

	# id = 0
        insert(P,v0);
        while (! is_empty(P)) {
            v = remove(P);
            v.status = VISITED;
            print v.name;
            foreach w in adj(v) {
                if (w.status == UNSEEN) {
                    # 必要的話, 可以記載...
                    # ++id;         # w 被發現的順序
                    # w.parent = v; # w 由誰介紹入 FRINGE
                    w.status = FRINGE;
                    insert(P,w);
                }
            }
        }

至於 P 究竟是什麼資料結構呢? 隨便。 如果採用 queue, 上述演算法就變成 queue-based search, 也就是 breadth first search 廣度優先搜尋; 如果採用 stack, 就變成 stack-based search, 可以算是 depth first search 深度優先搜尋 的一種, 都是先處理晚輩, 才回頭處理長輩。 (小小的不同: 標準的 DFS, 同一輩的 vertices 按照長幼順序處理; stack-based search, 同一輩的 vertices 則是先處理弟妹再處理兄姊。) 如果我們的目的只是希望將所有 vertices 點名一遍, 對於順序並沒有特別的要求, 用這兩種簡單的資料結構就足夠了。

不論選用那一種資料結構來存放 FRINGE, 進行 graph traversal 之後都會有一個副產品: 它的 spanning tree。 在進行 graph traversal 的過程當中, 可以幫每個 vertex w 記下當初介紹它進入 FRINGE 的是誰。 如果是 v 介紹 w 進入 FRINGE 的, 就稱 v 為 w 的 parent, 而稱 v->w 為一條 tree edge。 演算法結束之後, 所有的 tree edges 與 G 的所有 vertices 就是一個 spanning tree。 又, G 的其他 edges 都稱為 back edges。

Prim's Algorithm for Minimal Spanning Tree

上述演算法稍微加強, 可以用來找出一個 graph 的 minimal spanning tree。

第一個更改是: 大迴圈每次從 FRINGE 選一個出來變成 VISITED 時, 不再是簡單的先進先出或先進後出, 而是要看那一個 fringe vertex 指向 parent 的 edge 的數字最小, 就挑它。 記得嗎? 因為這些都將變成 spanning tree 的 tree edges, 所以當然要挑小一點的才好。

其次, 在處理 v 的所有鄰居時, 原先我們只處理 UNSEEN 的狀況; 但現在連 FRINGE 也要處理。 想像老鼠會的上下線關係: v 現在不只要介紹下游 (UNSEEN) 入會 (FRINGE), 還想要跟上游搶生意 -- 用更好的條件把身旁已入會 (FRINGE) 的一個 vertex w 搶過來, 讓自己變成它的介紹人。 因為 w 原先由別人 (w 的舊 parent) 介紹入 FRINGE 的 edge 可能比較貴; 如果改由 v 介紹入 FRINGE 確實比較便宜, 就應該改由 v 來當 w 的 parent, 也就是 w 指向 parent 的 tree edge 應該要更新。

最後修改資料結構。 既然我們對資料結構 P 的動作, 不外乎: 新增/刪除最小元素/測試是否為空, 我們根本就是把 P 當做一個 priority queue 在用。 而最適合實作 priority queue 的簡單資料結構, 莫過於 heap 了。 這個 heap 裡面放的是 FRINGE vertices, 而它們的 priority 則是指向 parent 的 tree edge 的 weight。 這樣修改資料結構, 對於結果的正確性沒有損益, 但是可以提升演算法的效率。

當然要注意到: 如果發生了更新 parent 的狀況, w 的 priority 也必須隨著更新, 所以必須記得做 upheap。

綜合以上, 得到如下的 Priority First Search 演算法:

	# id = 0
        insert(P,v0);
        while (! is_empty(P)) {
            v = remove(P);
            v.status = VISITED;
	    v.value = #priority#;
            print v.name;
            foreach w in adj(v) {
                if (w.status == UNSEEN) {
                    # 必要的話, 可以記載...
                    # ++id;         # w 被發現的順序
                    # w.parent = v; # w 由誰介紹入 FRINGE
                    w.status = FRINGE;
                    insert(P,w);
                } else if (w.status == FRINGE) {
                    new_prio = #priority#;
                    if (new_prio <= w.value) {
                        # w.parent = v; # 換個人介紹入會條件更好
                        w.value = new_prio;
                        update(P,w);
                    }
                }
            }
        }

PFS (Priority First Search) 演算法裡面的 #priority# 可以填入不同的運算式, 將得到不同的演算法。 以我們希望求 MST 而言, 這裡應該填入 "w 指向 v 那條 edge 的 weight", 所得到的演算法則稱為 Prim's algorithm for Minimal Spanning Tree

仔細的讀者會質疑: 每次都挑最小的 edge, 就能確保最後的 spanning tree 總和最小嗎? 這樣做不會太短視近利了一點嗎? 沒錯, Prim's algorithm 是一個短視近利的 greedy algorithm, 與其他的 greedy algorithms 一樣具有兩個特性: 計算過程很簡單; 困難處在於證明。 至於證明, 這裡就省略了。

Priority queue 用 heap 來實作, 則每個 insert, remove, update 的動作各花 O(log(|V|)) 的時間。 若用 adjacency list 來存 graph, 則最內層迴圈測試 unseen 的 if 總共會成功 |V| 次, 進行 insert; 至於測試 fringe 的 else if, 總共成功至多 |E| 次, 進行 update; 而 while 迴圈的 remove 則總共進行 |V| 次, 因此整個演算法總共耗時 O((|E|+|V|) log(|V|))。 如果我們討論的對象局限於 connected graph, 則 |V| 屬於 O(|E|), 所以上式可簡化為 O(|E|log(|V|))。

Dijkstra's Algorithm for Single-Source Shortest Path Problem

Priority-first search 也可以用來求 vertex 之間的最短路徑。 在一個 weighted graph 當中, 給定起點 a 與終點 z, 請問從 a 到 z 的最短路徑應該如何走? 距離是多少?

實際去解, 會發現欲求 a 到 z 的最短路徑, 不得不同時將 a 到 b, a 到 c, a 到 d, ... a 到 y 的最短路徑, 一併順便求出來。 所以乾脆以 a 為起點, 以其他每一點為終點, 一口氣同時回答 n 個問題。 這個問題稱為 Single-Source ShortestPath Problem。

至於演算法呢, 很簡單, 只要將上述的 PFS 演算法當中的 #priority# 改成 v.value + (edge v-w 的 weight) 就可以了。 現在每個 vertex v 的 value 欄位, 存的是 "從 a 到 v 的最短路徑距離"; 而最內層迴圈遇到 fringe node 是否要更改 parent 的判斷條件, 相當於 ... else if (v.value + edge(v,w) < w.value)

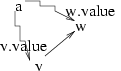
從 a 到 v 的距離, 加上 edge(v,w) 的距離, 是否小於從 a 到 w 的距離?

得到的演算法, 稱為 Dijkstra's algorithm for single-source shortest path problem, 仔細與 lcs 等問題對照, 會發現它其實可以算是 動態規劃 的一種。 (為了解大問題, 必須先列表將許多小問題的答案存起來。)

其實 BFS, DFS, Prim's algorithm, Dijkstra's algorithm 原先是各不相干的; 但 Robert Sedgewick 看出它們的相關性, 用一個演算法解決以上所有問題。

All-Pair Shortest Path

在一個 weighted graph 當中, 「從 x 出發, 要到 y 的最短路徑及其距離各是多少?」 對圖當中每一對 vertices 都問這樣的問題。

可以使用上節的 Dijkstra's algorithm, 從不同的 vertex 出發各問一次, 即可得到答案。

另解: Floyd-Warshall algorithm

        foreach a in V {
            foreach x in V {
                foreach y in V {
                    if (min[x][a] + min[a][y] < min[x][y]) {
                        min[x][y] = min[x][a] + min[a][y];
                        via[x][y] = a;
                    }
                }
            }
        }

注意: 中繼站 a 由 最外層 的迴圈控制!

以矩陣表示法徒手操作: 從原矩陣開始, 沒有 edge 的地方填無限大 (表示目前還不知道有路可以通達). 執行以下動作 |V| 步:

  1. 第 i 步時, 以第 i 列第 i 行的元素 (a-a) 作為長方形的一個角。
  2. 對矩陣內的每一元素 x-y, 都做以下動作: 以 x-y 為長方形的對角, 找出剩下的兩角 (x-a 與 a-y)。 若這兩角 (x-a 與 a-y) 數字和比對角 (x-y) 數字小, 則以此和取代之。

第 1 步做完後, 矩陣內 x-y 位置的值代表: 「若只允許以 a 為中繼站, x 到 y 的最矩距離為多少?」 第 2 步做完後, 矩陣內 x-y 位置的值代表: 「若只允許以 a,b 為中繼站, x 到 y 的最矩距離為多少?」 第 3 步做完後, 矩陣內 x-y 位置的值代表: 「若只允許以 a,b,c 為中繼站, x 到 y 的最矩距離為多少?」 ...

除了記載最短距離, 如何記載最矩路徑? 用一個 |V|*|V| 的矩陣記載「從 x 到 y, 最後因為使用了那個中繼站 (姑且稱之為 a), 而得到最矩路徑?」 最後可以遞迴地找出 x 到 a 及 a 到 y 的最矩路徑...

時間複雜度: O(|V|^3)

請將 algotutor 的資料檔餵給範例程式 flwa 吃, 像這樣: flwa lv.gr 並重複執行
    algotutor -a dijk -s x1 lv.gr
    algotutor -a dijk -s x2 lv.gr
    algotutor -a dijk -s x3 lv.gr
    ...

核對結果是否相符。 Q: flwa 的答案當中, 對角線上的元素, 其值有何意義?

同樣的演算法, 若用於不具 weight 的 graph, 並以 or 運算取代比較大小的運算, 則得到 Warshall's algorithm for computing transitive closure。

Maximal Flow/Minimal Cut

  1. Maximal Flow
  2. A Labeling Algorithm for the Maximum-Flow Network Problem
  3. Jong C. Park. Network Models